
Read data
When using Factor to analyze data, you will need the participants' scores to some observed variables. For example, you may have the scores of 1,500 participants for a test of 10 items. The data must be stored in a file in ASCII format. The scores of each participant correspond to the rows in the file, while participants' answers to each item correspond to the columns in the file. Each column has to be spaced by at least one character: a space character, a tab, a coma, a : character, or a ; character. If you have your data in EXCEL, you may want to use this excel file to preprocess the data and save it in ASCII format (please, note that you must allow macros in order to preprocess the data).
The contents of the ASCII file for this example would be:
2 |
2 |
2 |
2 |
1 |
2 |
2 |
2 |
3 |
2 |
|---|---|---|---|---|---|---|---|---|---|
1 |
2 |
1 |
2 |
1 |
1 |
3 |
2 |
3 |
2 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
2 |
3 |
2 |
2 |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
2 |
3 |
2 |
2 |
1 |
2 |
2 |
2 |
2 |
1 |
where the last row contains the answers reported by the last participant. Note that the presence of missing data are allowed: a code value must be used to indicate the presence of a missing data. FACTOR by defauls uses the code value 999. Missing values are managed following the proposal by Lorenzo-Seva & Van Ginkel (2016): multiple imputation of missing data in exploratory factor analysis. The number of datasets imputed is 5, and the imputation is based on Hot-Deck imputation. If FACTOR finds incomplete rows, the whole row is dismissed from the analysis.
The data are read from the ASCII file by clicking on the Read Data button in the main menu (see details). This button opens the menu that helps to read the data.
When bootstrap sampling is allowed by the user, confidence interval of a large number of indices is reported. If the bootstrap sampling is allowed, robust factor analysis is also base on bootstrap sampling techniques; in addition, robust factor analysis is also base on analytical estimates (however, confidence intervals will not be computed). Our advice is to allow bootstrap sampling to be computed. The menu is now shown ready to read an ASCII file (y.dat) where the answers of 500 participants to 14 items were previously stored; in additon, bootstrap sampling thecniques are allowed, and the missing value is defined as 999:
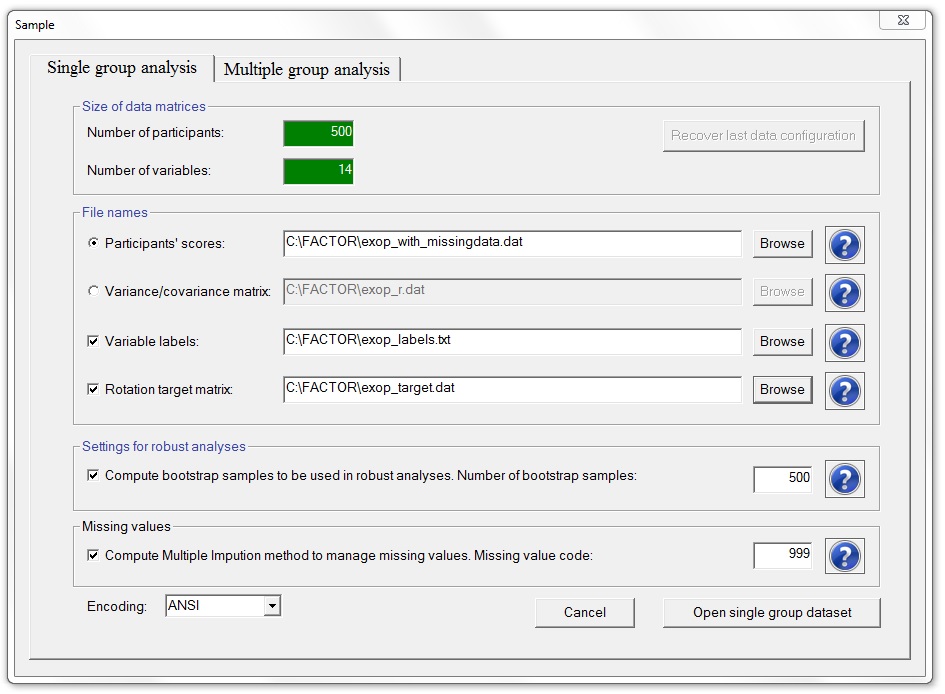
Please, note that a correlation matrix can also be read from disk. In this case, the matrix must be a square matrix. If this option is used, the program will not be able to compute all the indices avaible when raw data is used.
Variable labels are allowed. It must be a text file, where each rows corresponds to the labels of each variable. FACTORS expects to find as many rows, as variables. Labels with more than 40 characters are cut to be of 40 characters. The labels are used in the output report.
Finally, a rotation target matrix is also allowed. It must be a text file. The target matrix can be fully specified (i.e., each value in the target indicates the expected value in the loading matrix after rotation) or semi-specified (i.e., only some values in the target matrix indicate the expected value in the loading matrix after rotation). Typically, the specified values are the ones expected to be zero (or as close as possible to zero) in the loading matrix after rotation. The non-specified values are indicated with values of +9 (non-specified value that is expected to be larger than zero) or -9 (non-specified value that is expected to be lower than zero). Here you have an example of a semi-specified target matrix:
9.0 |
0.0
|
9.0
|
0.0
|
-9.0
|
0.0
|
9.0
|
0.0
|
-9.0
|
0.0
|
-9.0
|
0.0
|
9.0
|
0.0
|
0.0
|
-9.0
|
0.0
|
9.0
|
0.0
|
-9.0
|
0.0
|
9.0
|
0.0
|
9.0
|
0.0
|
9.0
|
0.0
|
-9.0
|
If this target matrix is properly read, the following menu will help you to check that non errors were found:
Please note that, in order to use the target matrix during the rotation, the number of factors (or components) retained must coincide with the number of columns of the target matrix.
When a single group dataset is loaded and the sample is at least of 400 observations (i.e., the number of rows is larger than 399), two subsamples are computed using Solomon method. Solomon algorithm optimally splits the data in two equivalent halves, and improves the representativeness of the subsamples (i.e., all possible sources of variance are enclosed in the subsamples). The aim is to allow the researcher to have two subsamples to run different analyses in each subsample. For example, the first subsample could be used to run a fully exploratory analysis based on a rotation to maximize factor simplicity (like Promin); and the second subsample could be used to run a second analysis with a confirmatory aim based on an oblique Procrustean rotation using a target matrix build as suggested by the outcome of the first fully exploratory analysis. FACTOR allows the researcher to save the new dataset that includes the group variable, so that new analyses can be started from this file.